벡터와 좌표계
(1) 평면 벡터
$R^2$에서 크기(스칼라)와 방향의 의미를 모두 포함하는 표현 도구

여기에 있는 $A(a_1, a_2)$는 점의 좌표가 아니라 벡터이며, $x$가 $a_1$만큼 변할 때 $y$는 $a_2$만큼 변한다는 정보를 준다.
벡터의 정의는 크기와 방향에 대해서만 이야기 하므로, 벡터의 시점(시작점)과 종점은 중요하지 않다. 즉, 두 벡터를 비교할 때, 시점과 종점이 다르더라도 크기와 방향만 같으면 같은 벡터로 본다.

예를 들어, 위 그림에서 v와 같은 벡터를 찾아보자.
| 방향 같다 | 크기 같다 |
| a, d | c, d |
방향도 같고, 크기도 같은 d가 같은 벡터다.
(2) 공간 벡터
$R^3$에서 크기와 방향의 의미를 모두 포함하는 표현 도구
축이 세 개이므로 순서쌍도 세 개가 있다.
(3) n차원 벡터
$R^n$ 상의 벡터 $v=(v_1, v_2, v_3, ..., v_n)$
$\vec{AB}=(b_1-a_1, b_2-a_2, ... , b_n-a_n)$
두 n차원 벡터가 서로 같으려면 두 벡터의 각각의 원소가 서로 같아야 한다.
벡터의 연산
(1) 노름
- 벡터의 크기 (또는 길이)라고도 하며, $\lVert v \rVert = \sqrt{v_1^2+v_2^2+...+v_n^2}$
ex) $v(2,1) => \lVert v \rVert = \sqrt{2^2+1^2}=\sqrt{5}$ - 노름이 1인 벡터를 단위벡터라고 한다.
정규화 : ${v \over \lVert v \rVert}$
정규화 한 것을 $\hat{v}$로 표기한다.
ex) $v(2,1) => \hat{v}=({2 \over \sqrt{5}}, {1 \over \sqrt{5}})$ - $e_1=(1,0,...,0), e_2=(0,1,...,0)$ 등을 표준단위벡터라고 한다.
$v=(v_1, v_2, ... v_n)$일 때, 표준단위벡터를 사용하여, $v_1e_1+v_2e_2+...+v_ne_n$으로 표현 가능(벡터의 선형 결합)
(2) 선형결합
선형은 단순히 직선을 의미하는 것이 아니다. 곡선의 형태를 띄면서도 선형일 수 있다.
벡터의 덧셈과 뺄셈

뺄셈의 경우에는 방향을 뒤집어 덧셈을 수행한다.
벡터의 실수배

선형(일차)결합
$R^n$의 벡터 $w$가 임의의 실수 $k_1, k_2, ... k_r$에 대하여
$w=k_1v_1+k_2v_2+...+k_rv_r$의 형태로 쓰여지면, $w$를 $v_1,v_2, ... v_r$의 선형(일차)결합이라 한다.
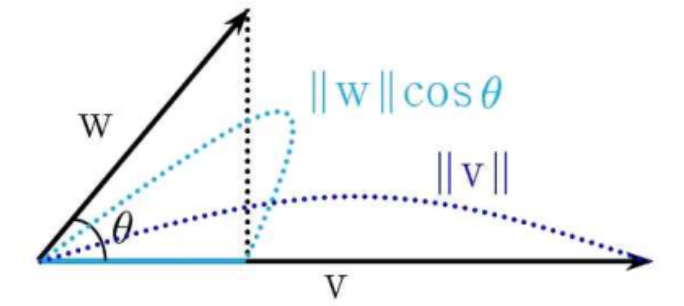
(3) 스칼라곱
벡터의 곱은 두 가지 방식이 있다. 첫 번째는 그 결과가 스칼라(크기)인 스칼라곱, 두 번째는 그 결과가 벡터인 벡터곱이 있다. 스칼라곱은 한 벡터가 다른 벡터의 방향에 얼마만큼의 스칼라(크기)를 가하는가를 말한다.
$$w=\lVert v \rVert \lVert w \rVert cos\theta=v_1w_1+v_2w_2+...+v_nw_n$$
($\theta$는 $v,w$가 이루는 각)

* 벡터의 연산 성질

(4) 벡터곱
다른 벡터를 얻어내는 연산. 3차원 공간에서만 정의된다.
방향은 두 벡터에 동시에 수직이고, 크기는 두 벡터의 평행사변형의 면적인 $R^3$ 상의 벡터.
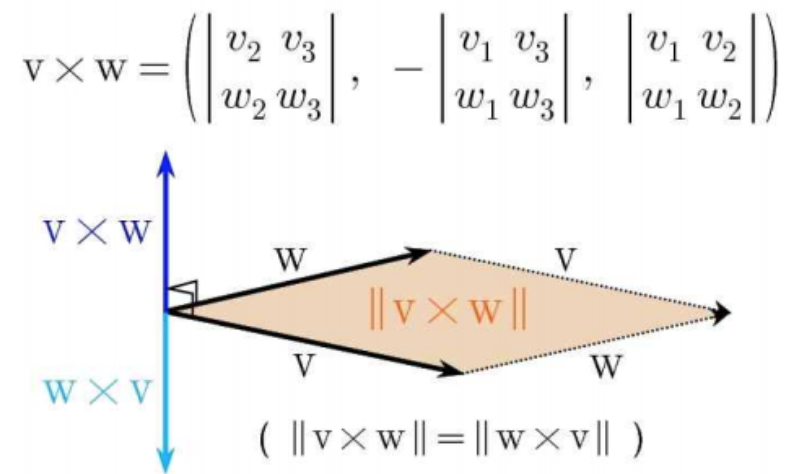
$\begin{vmatrix} v_2 & v_3 \\ w_2 & w_3 \end{vmatrix}$는 행렬식(Determinant)이다.
ex) $v=(2,0,0), w=(0,3,0)$일 때, $v \times w=(0,0,6)$이다.
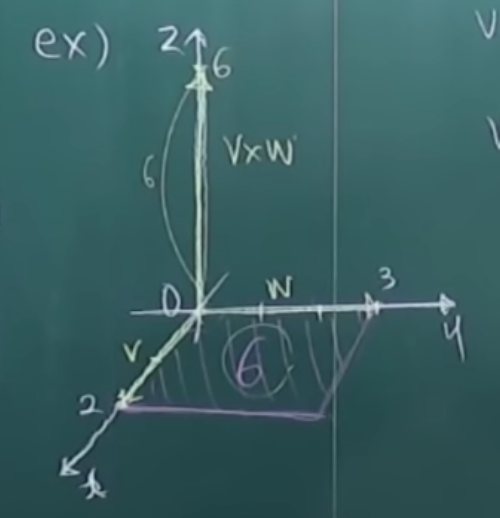
* 참고
벡터의 방향은 오른 나사의 법칙을 적용해 알아낼 수 있다. 위 예제는 $v \times w$이므로 $v$에서 시작해 $w$로 가는 방향으로 오른손을 감을 때, 엄지의 방향이 벡터의 방향이 된다.
* 벡터의 곱의 성질

벡터의 응용
(1) 직선의 표현
$R^2$ 또는 $R^3$에서 위치벡터(원점을 시점으로 하는 벡터)가 a인 점 A를 지나며 방향벡터(직선이 나아가는 방향을 지시하는 벡터) v인 직선 상의 임의의 점 X의 위치벡터 x는 $X=a+kv$를 만족한다.(단, k는 임의의 실수)
ex 1)

$a=(-1, 1), v=(1,1), X=(x,y)$일 때, 위 식에 대입을 해보면, $(x,y)=(-1,1)+k(1,1)=(-1+k, 1+k)$
$x=-1+k => k=x+1, y=1+k => k=y-1$
$y=x+2$
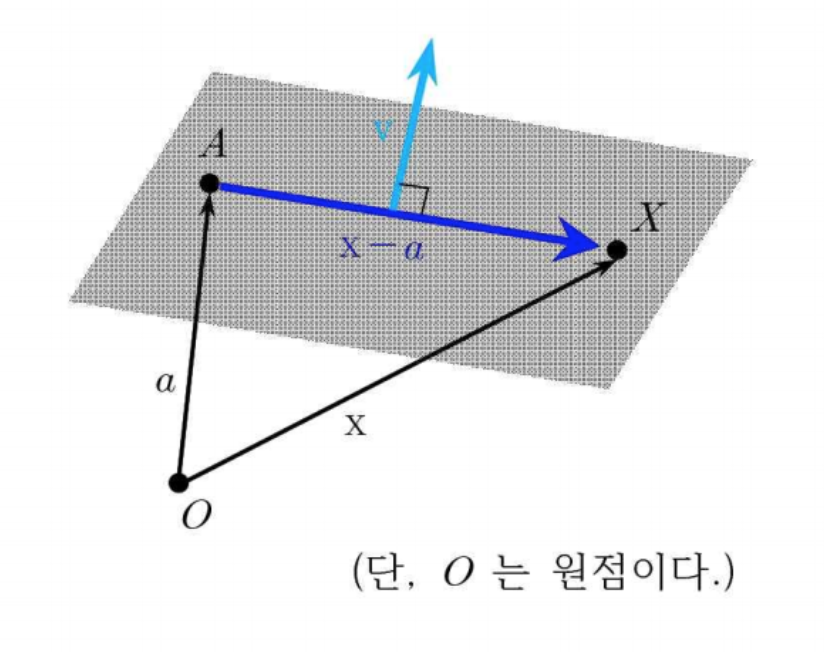
(2) 평면의 표현
$R^3$에서 위치벡터가 a인 점 A를 지나며 법선벡터(평면에 수직인 벡터)가 v인 평면상의 임의의 점 X의 위치벡터 x는 $(X-a) \cdot v=0$을 만족한다.(x-a와 v는 수직이므로 스칼라곱을 하면 $cos \theta = 0$이기 때문에 0이 된다.)
* 법선벡터는 평면 상의 서로 다른 두 직선의 방향벡터들의 벡터 곱으로써 구하면 용이하다.
ex)
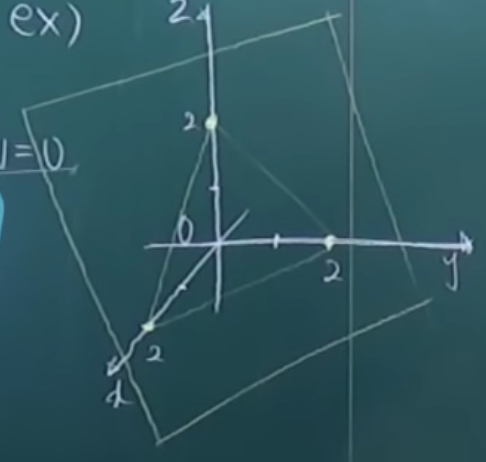
위 그림처럼 $a(2,0,0), b(0,2,0), c(0,0,2)$이 있을 때, 주어진 법선벡터가 없으므로 두 방향벡터의 외적으로 구해야 한다. $u_1=ab=(-1,1,0), u_2=ac=(-1,0,1)$. 그러므로 $v=(1,1,1)$이 법선벡터임
임의의 점 $a=(2,0,0)$을 사용할 때, $(x-a) \cdot v=0$ => $(x-2, y, z) \cdot (1,1,1)=x-2+y+z=0$이 평면의 방정식이다.
'강의록 > 이상엽Math 선형대수학' 카테고리의 다른 글
| 3강 수학적 벡터 (벡터공간) (0) | 2020.01.12 |
|---|---|
| 1강 행렬과 행렬식 (0) | 2020.01.04 |
| 0강 수학의 절반. 선형대수 (0) | 2020.01.01 |

