개요
해시 테이블(Hash Table)은 많은 양의 데이터의 인덱싱(indexing)을 빠르게 해 줌으로써 탐색(Search), 삽입(Insert), 삭제(Delete)의 속도를 높여주는 자료구조다. 그렇기 때문에 해시 테이블은 Database indexing, Caching, Error checking, Password authentication 등 많은 곳에서 쓰이고, dynamic set을 구현하는 데 사용되기도 한다.
자료 출처
1. Hash Tables and Hash Functions
3. Introduction to Algorithms third edition 11장
해시 테이블

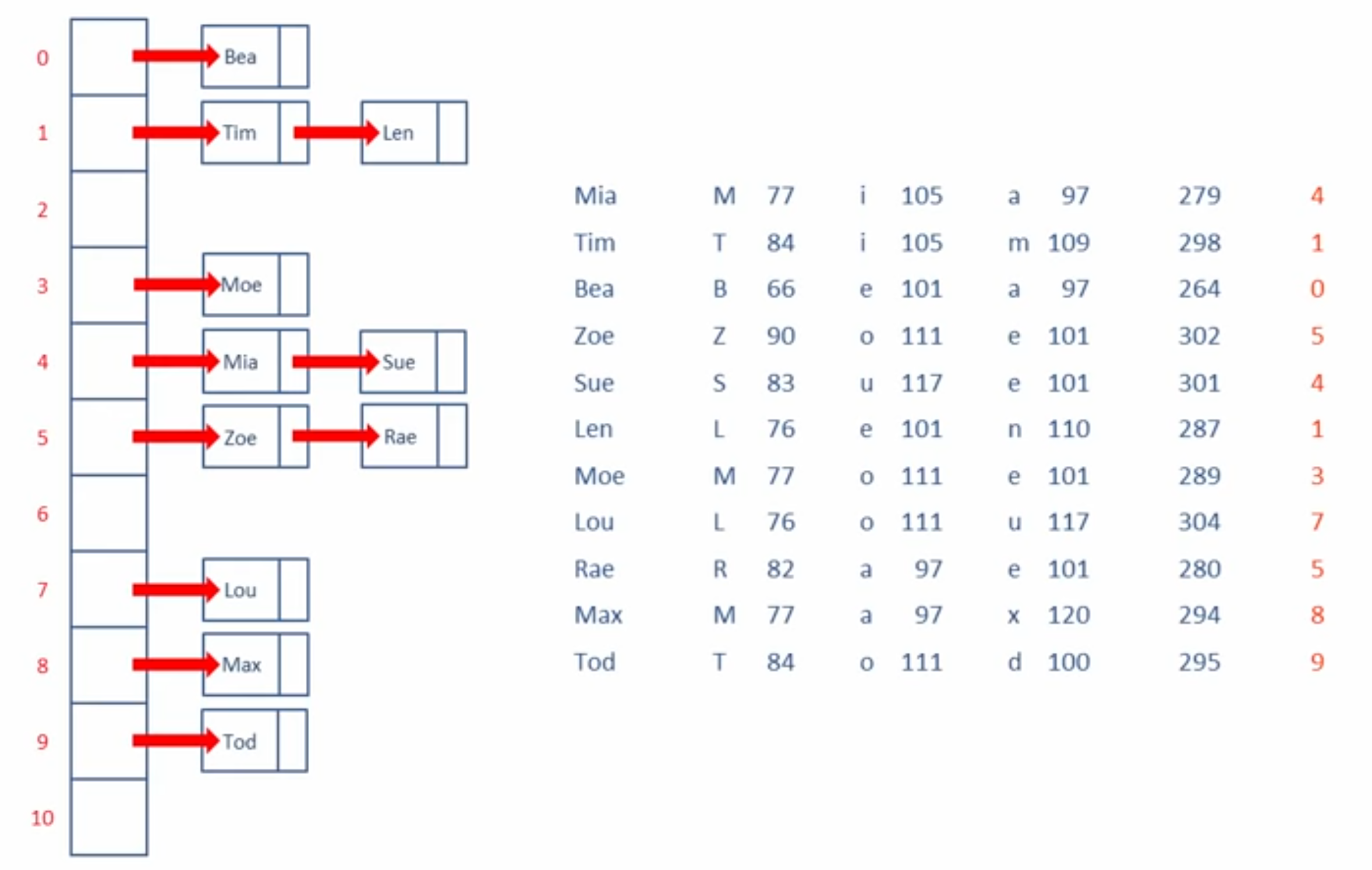
위의 배열에서 'Ada'를 찾는 프로그램을 만든다고 하자.
보통 0번째 배열부터 찾고자 하는 문자열을 발견할 때까지 비교해나가는 방법으로 프로그램을 만든다. 이 예와 같이 원소의 수가 11개인 경우에는 빠르게 할 수 있지만 원소의 수가 커질수록 이 프로그램의 탐색 속도는 느려진다(O(n)이기 때문). 하지만 찾고자 하는 Ada라는 문자열 자체에서 인덱스인 8을 추론할 수 있다면, 원소가 얼마나 많든 탐색 하는데 O(1)의 시간만 있으면 된다.(각 char의 ASCII 코드를 더한 값을 배열의 크기로 나눈 나머지 값을 인덱스로 사용하였다)

위 배열에서는 기존에 있던 사람의 이름(key) 뿐만 아니라 생년월일, 국적, 직업과 같은 부속 데이터(satellite data)가 함께 있는 것을 확인할 수 있다. 즉, 해시 테이블은 (이 예제에서는) 이름을 키(key)로 활용해 상수 시간(Constant time) 안에 인덱싱하고 필요하다면 부속 데이터에도 접근하는 자료구조다.
해시 테이블은 T로 표현된다.
해시 함수(Hash Function)
큰 수나 복잡한 문자열로 이루어진 키(key)를 비교적 간단한 인덱스 넘버(index number)로 변환시켜 키가 해시 테이블의 어디에 위치시켜야 하는지 알려주는 알고리즘이다.
위에서 봤던 예제에서 'Ada'를 8이라는 정수로 변환시킨 것도 해싱 알고리즘이다.
해시 함수는 h를 사용하여 표현하며 키 k를 T[h(k)]에 저장한다. 이때 키 k가 h(k)로 해싱되었다고 말한다.
충돌(Collisions)
위에서 봤던 예제에서는 각 키(key)의 해시값을 구해보니 운이 좋게도 서로 다른 값이 나왔다. 그래서 하나의 주소 값에 하나의 원소만 들어갈 수 있었다.
하지만 두 키가 같은 위치에 해시되는 문제가 발생할 수 있는데(즉, 키 k1, k2에 대해서 h(k1) == h(k2)인 상황), 이것을 충돌(Collisions)이라고 한다. 가장 이상적인 방법은 충돌을 완전히 피하는 것이다. 그러나 일반적으로 키의 개수가 해시 테이블의 원소의 수보다 많은 경우가 많으므로 충돌을 완전히 피한다는 것이 불가능하다. 그렇기 때문에 적절한 해싱 알고리즘을 선택해 충돌의 횟수를 최소화하고, 충돌이 일어났을 때의 어떻게 대처할지 정해야 한다.
충돌 해결 방법에는 크게 두 가지가 있다.
- 체이닝
- 개방 주소화
체이닝(chaining)
체이닝은 위 그림과 같이 같은 위치에 해시되는 데이터를 같은 연결 리스트에 넣는 것이다.
시간 복잡도
우리가 삽입, 탐색, 삭제할 연결 리스트의 길이를 n이라고 하자.
삽입의 경우 키를 연결 리스트의 가장 앞에 넣는지 혹은 뒤에 넣는지에 따라 시간 복잡도가 달라지고, 키의 중복을 허용하는지에 따라 시간 복잡도가 달라진다.
| 연결 리스트의 앞 | 연결 리스트의 뒤 | |
| 키 중복 허용 O | O(1) | O(n) |
| 키 중복 허용 X | O(n) | O(n) |
연결리스트의 가장 뒤에 넣는 방법으로 삽입하면 해당 연결 리스트에 저장된 원소의 수만큼 시간이 걸린다(O(n)). 반면 가장 앞에 넣으면 O(1)의 시간이 있으면 된다. 그림에서는 가장 뒤에 넣는 것을 보여준다.
키의 중복을 허용하지 않는다면 어떻게 삽입하든 연결 리스트 전체를 탐색해서 중복 키가 있는지 확인해야 하기 때문에 O(n)의 시간이 걸린다.
탐색의 경우에 O(n)의 시간 복잡도를 가진다.
삭제는 인자(parameter)로 데이터 자체를 넘겨 인자의 왼쪽 포인터와 오른쪽 포인터를 이어주는 방식으로 작동한다. 단방향 연결 리스트인 경우와 양방향 연결 리스트인 경우의 시간 복잡도가 달라진다. 양방향 연결 리스트인 경우에는 데이터 자체에 왼쪽 값의 포인터와 오른쪽 값의 포인터가 저장되어 있으므로 그것들을 서로 연결시켜주기만 하면 되므로 O(1)의 시간이 필요하다. 반대로 위 그림과 같이 단방향 연결 리스트인 경우에는 삭제할 원소의 오른쪽 값은 알지만 왼쪽 값은 모르므로 최악의 경우 O(n) 만큼의 탐색을 수행해야 한다.
최악의 경우에는 모든 키가 하나의 연결 리스트에 해싱될 수 있다. 이 경우에는 길이가 K인 하나의 연결 리스트가 만들어지며(키의 개수를 K라 가정), 최악의 경우 O(K) + O(1)(해시 함수 수행 시간)의 시간 복잡도를 가진다.
그렇다면 키 값이 잘 분산되었을 경우에 시간 복잡도는 어떨까?
위에서 간단하게 봤듯이 체이닝을 이용한 해싱의 평균 성능은 해싱 알고리즘이 키 값을 얼마나 잘 분산시키느냐에 달려 있다. 해싱 알고리즘을 잘 작성하는 방법은 나중에 다루기로 하고 지금은 데이터들이 해시 테이블에 모든 위치에 균등한 확률(equally likely)로 해시되며, 독립적(independently)으로 해시된다고 가정하자. 이 가정을 단순 균등 해싱(SUHA, Simple Uniform Hashing Assumption)이라고 한다. (해시 함수는 랜덤 함수가 아니기 때문에 현실에서는 불가능한 가정이지만 성능 분석을 위해 주로 하는 가정이다. 사실 유니버설 해싱(universal hashing)이라고 부르는 랜덤화 된(randomized) 해시 함수를 사용하는 기법이 있기는 하나 여기에서는 다루지 않는다.)
단순 균등 해싱을 가정하면 해싱 알고리즘의 성능은 적재율이 결정한다. m개의 저장 공간(연결 리스트)을 가지고 있고, n개의 데이터가 저장된 해시 테이블 T에서 T의 적재율(Load factor) α를 n / m으로 정의한다. α는 1보다 작을 수도, 같을 수도, 클 수도 있다.
탐색을 할 때를 생각해보면, 탐색은 해시 값을 계산하는 것, 해시 값이 가리키는 곳의 연결 리스트에서 원하는 데이터를 찾는 것으로 나눌 수 있다. 해시 값을 계산하는 것이 O(1)이고, 연결 리스트에서 원하는 데이터를 찾는 것은 O(α)이다. 그러므로 탐색을 할 때는 O(1 + α)의 시간 복잡도를 가진다고 할 수 있다. 즉, 평균적으로 상수 시간의 시간 복잡도를 가진다.
체이닝에 사용하는 연결 리스트가 양방향 연결 리스트일 경우 삽입과 삭제는 최악의 경우 O(1)의 수행 시간을 필요로 하기 대문에 평균적으로 O(1)에 모든 작업을 수행할 수 있다.
개방 주소화
체이닝과 달리 테이블 외부에 저장된 데이터 없이 모든 데이터를 해시 테이블 그 자체에 저장하는 방법을 개방 주소화 방법(open-addressing)이라고 한다. 외부에 데이터가 없으므로 해시 테이블이 꽉 차서 더 이상 삽입이 가능하지 않을 수도 있다. 즉, 적재율이 1을 넘을 수 없다.
개방 주소화 방법의 장점은 포인터를 전혀 사용하지 않는다는 것이다. (대신 조사될 위치의 순서를 계산한다) 포인터를 저장하지 않음으로써 얻어진 추가 메모리는 해시 테이블의 저장 공간 확장에 이용될 수 있다. 이것은 결과적으로 충돌을 줄이고 빠른 접근을 가능하게 한다.
개방 주소화 방법에서 삽입을 수행하기 위해서는 키를 저장할 빈 공간을 찾을 때까지 해시 테이블을 탐색해야 한다. 탐색 방법은 선형 탐색, 2차원 탐색, 중복 해싱. 이렇게 세 가지가 있다. 이 방법들은 탐색, 삭제를 할 때도 똑같이 사용된다.
선형 탐색
선형 조사(linear probing)는 T[h(k)]부터 T[m - 1]까지 조사하고, 앞으로 돌아가 T[0]부터 T[h(k) - 1]까지를 조사한다. 선형 조사는 구현하기 쉽지만 1차 군집(primary clustering)이라는 문제가 있다. 1차 군집은 데이터가 연속적으로 길게 저장되면 체증을 일으켜 평균 탐색 시간을 증가시키는 것을 말한다.

2차원 탐색(= 제곱 탐색)
충돌 발생 시 $h(k) + 1^2$, $h(k) + 2^2$, $h(k) + 3^2$, ...의 순서로 탐색을 시도하는 것이다. 선형 탐색보다는 군집을 덜 일으키긴 하지만, 두 개의 키가 같은 초기 조사 위치를 가지면 그 조사 순서도 같기 때문에 2차 군집(secondary clustering)이라 불리는 다소 가벼운 군집을 초래한다.
단, 이것은 2차원 탐색의 한 예이고 $ai^2 + bi + c$의 형태로 나타낼 수 있기만 하면 된다. a, b, c는 상수.
중복 해싱(= 이중 해싱)
중복 해싱(double hashing)은 해시 값에 무작위성을 부여해 clustering을 방지하기 때문에 개방 주소화 방법에서 가장 좋은 방법 중 하나다. 수식으로 표현하자면 다음과 같다.
$$h(k, i) = (h_1k + ih_2k) \% m$$
즉, 해시 함수를 두 개 사용한다.
초기 조사는 T[$h_1(k)$]에서 이루어지고, 충돌이 일어났을 때는 $ih_2(k)$를 사용해 다음에 탐색할 곳의 위치를 알아낸다. 이렇게 하면 초기 조사 위치가 같더라도 오프셋( = 탐사 이동폭)이 다르고, 오프셋이 같다러도 초기 조사 위치가 달라지기 때문에 1, 2차 군집을 예방할 수 있다.
다만 이때 $h_2(k)$의 값은 해시 테이블의 크기인 m과 서로소여야 한다. 오프셋인 $h_2(k)$와 m이 서로소가 아니라면 탐색을 아무리 해도 탐색이 닿지 않는 영역이 있기 때문이다.(이 조건을 보장하는 쉬운 방법은 m이 2의 지수승이 되게 하고 $h_2$가 항상 홀수 값을 생성하도록 설계하는 것이다. 다른 방법은 m이 소수 값을 갖게 하고 $h_2$가 항상 m보다 작은 양의 정수가 되도록 설계하는 것이다.)
아래 그림은 중복 해싱을 이용한 삽입의 예를 보여준다.

해시 함수로 $h_1 = k \% 13$과 $h_2(k) = 1 + (k \% 11)$을 사용하는 크기가 13인 해시 테이블을 이용한다. 초기 조사 위치인 1번째와 다음 조사 위치인 5번째가 이미 점유되어 있다고 확인한 후 빈 위치인 9번째에 키 14를 저장한다.
개방 주소화 방식의 문제점
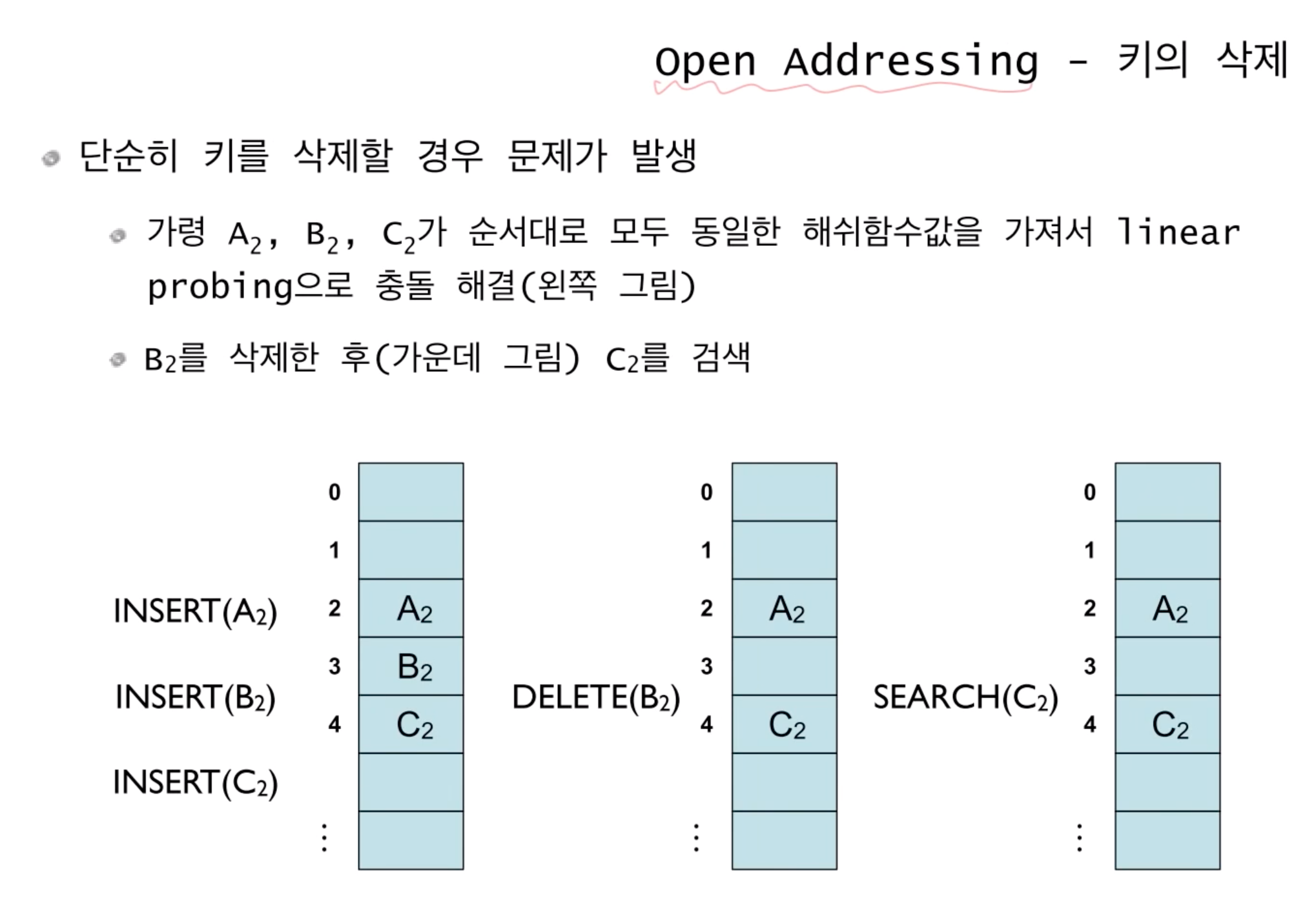
선형 탐색으로 탐색했을 때의 예시다. 만약 A2, B2, C2의 해시 값이 모두 2라면, 왼쪽 그림과 같이 2, 3, 4번에 위치하게 된다. 중간 그림처럼 B2를 삭제했다고 하자. 그리고 오른쪽 그림처럼 C2를 찾을 때, 먼저 2번과 비교해 값이 다르므로 3번을 보는데, 이때 값이 없으므로 C2가 없다고 판단하게 된다. C2는 테이블에 있으므로 이것은 사실이 아니다. 이것이 개방 주소화 방법의 문제점이다.
이를 해결하기 위한 방법은 두 가지가 있다.
첫 번째는 데이터를 지우고 나서 'DELETE' 마크를 해두는 것이다. 탐색할 때 자료가 없더라도 DELETE 마크가 있으면 '자료가 있었다가 지워진 것이므로 더 탐색하면 원하는 자료를 찾을 수 있다'는 것을 알 수 있다.
이 방법으로 문제를 해결할 수는 있지만 그렇게 좋은 아이디어는 아니다. 삽입과 삭제를 빈번하게 해서 대부분의 테이블이 DELETE로 마크되어 있다면, 탐색을 할 때 적당한 지점에서 멈출 수 없고, 테이블 전체를 확인해야 내가 찾는 키가 있는지 없는지를 확인할 수 있다.
두 번째는 삭제한 데이터의 뒤에 있는 데이터들의 인덱스를 하나씩 앞으로 당기는 것이다. 예를 들어, 3번째 위치에 있는 키를 삭제했다면 4번째에 위치한 키를 3번째로 옮기는 것이다. 해시 테이블의 크기가 크다면 인덱스를 하나씩 당기는 것에 시간이 오래 걸릴 수 있다.
좋은 해시 함수란?
앞서 해시 함수에 대해 간단하게 살펴봤다. 충돌 문제를 해결하면서 단순 균등 해싱에 가깝도록 하는 것이 체이닝이든 개방 주소화든 해시 테이블의 성능을 높이는 데 중요한 역할을 한다는 것을 알게 되었다. 즉, 균등한 확률(equally likely)로, 독립적(independently)으로 해시되는 것이 좋은 해시 함수다.
그렇다면 어떻게 해야 이 조건을 만족하는 해시 함수를 만들 수 있을까
먼저 현실에서는 키들이 않다는 것을 알아야 한다. 즉, 키들은 특정한 패턴을 가진다. 예를 들어, 주민등록번호를 키로 사용한다면 93년대생의 경우 93으로 시작하는 키가 되는 것이다. 키들이 이러한 패턴을 가지더라도 해시 함수 값이 불규칙적이게 되도록 하는 것이 좋다.
만약 키들의 통계적 분포에 대해 알고 있어서 이 사전 지식을 활용해 해시 함수를 만들 수는 있겠지만, 키의 생성에 모든 패턴을 파악하는 것은 어렵기 때문에 통계적 분포를 고려한 해시 함수 작성은 현실적으로 어렵다.
그렇기 때문에 해시 함수 값은 키의 특정 부분에 의해서만 결정되어서는 안 되도록 해시 함수를 작성해야 한다. 즉, 키의 모든 부분이 해시 값을 결정하는 데 골고루 사용되도록 해야 한다. 그렇다면 두 키가 아주 작은 부분만 다르더라도 그 작은 부분이 영향을 미쳐 해시 값은 달라진다.
지금부터 배울 기법들은 키의 모든 부분이 해시 값을 결정하도록 하는 것들이다.
Division 기법
h(k) = k % m
나머지 연산을 해서 해시 값을 결정하는 것이다. 단점으로는 어떤 m에 대해서 해시 함수 값이 키값의 특정 부분에 의해서 결정되는 경우가 있다. 예를 들어, $m = 2^p$의 경우 키의 하위 p비트가 해시 값이 된다. 그래서 Division 기법은 홀로 쓰이는 경우는 거의 없고, 계산 결과의 마지막에 m으로 나머지 연산을 하면 0...m-1의 값이 나오기 때문에 인덱싱을 하기 쉽게 만들기 위해 쓰인다.
Multiplication 기법
다음과 같은 단계로 진행된다.
- 0과 1 사이의 상수 A를 선택한다.
- kA의 소수 부분만을 택한다.
- 소수 부분에 m을 곱한 후 소수점 아래를 버린다.
m = 8, word size = 5, k = 21일 때 해시 값을 구해보자.
- A를 13/32라고 하자.
- kA = 21 * 13 / 32 = 273 / 32 = 8 + 17/32이다. 여기서 소수 부분은 17/32
- 8 * 17 / 32 = 17 / 4 = 4.XXXX이므로 소수점 아래를 버리면 h(21) = 4
2번 과정을 보면 kA에서 소수 부분만을 선택하는 것이 있는데, 이 과정 때문에 키 값이 아무리 유사하더라도 해시 값을 예측하기는 어려워진다.
'자료구조 & 알고리즘' 카테고리의 다른 글
| [std]set, map (0) | 2019.05.10 |
|---|---|
| 에라토스테네스의 체 (0) | 2019.05.10 |
| 마스터 정리(Master Theorem) (0) | 2019.05.08 |
| 이진 검색 트리(Binary Search Tree) (0) | 2019.05.06 |
| 힙정렬(Heap Sort) (0) | 2019.05.01 |
