자료 출처
1. [알고리즘] 제11-1강 이진검색트리(Binary Search Tree)
4. Introduction to Algorithms 12장
트리라는 자료구조는 보통 데이터 자체가 계층적인 구조를 가지고 있을 때 주로 사용한다. 이를테면 조직도, 가계도가 있다.
하지만 검색 트리는 조금 다르다. 검색 트리에 저장되는 데이터들은 반드시 계층적인 구조를 가지고 있을 필요는 없으며, 검색 트리는 데이터를 저장하는 컨테이너로서 역할을 한다. 다른 컨테이너 역할을 하는 자료구조들과 다른 점은 검색 트리는 삽입(Insert), 탐색(Search), 삭제(Delete)와 같은 동적 집합(dynamic set) 연산을 많이 사용할 경우에 사용된다. (최대값, 최소값, successor, predecessor 등도 포함됨) 사전(dictionary) 및 우선순위 큐(priority queue)로 사용할 수도 있다.
아래에서 드는 예시에서는 편의성을 위해 키(key)만을 나타냈지만 실제로는 부속 데이터(satellite data)도 노드에 함께 저장되어 있다.
검색 트리의 필요성을 느껴보기 위해 검색 트리 말고 배열과 연결 리스트를 이용하여 저장된 데이터의 삽입, 탐색, 삭제를 해보자.
| 탐색 | 삽입 | 삭제 | ||
| 배열 | 정렬 O | O(lgn) | O(n) | O(n) |
| 정렬 X | O(n) | O(1)(O(n)) | O(1) | |
| 연결 리스트 | 정렬 O | O(n) | O(n) | O(1) |
| 정렬 X | O(n) | O(1) | O(1) |
삭제의 경우에는 삭제할 원소를 찾는 데 걸리는 시간은 제외하고, 순수하게 삭제하는 데 걸리는 시간만 포함한다.
배열이 정렬되어 있을 경우에는 탐색을 할 때 이진 검색을 할 수 있으므로 lgn 만큼의 시간만 있으면 된다. 삽입을 할 때는 삽입할 위치를 찾고 그 뒤에 있는 원소들을 뒤로 한 칸씩 미뤄야 하므로 n 만큼 시간이 걸리며, 마찬가지로 삭제를 할 때도 삭제한 원소의 뒤에 있는 원소들을 한 칸씩 앞으로 당겨야 하므로 n만큼의 시간이 걸린다.
배열이 정렬되어 있지 않은 경우에 삽입을 한다면 맨 앞이나 맨 뒤에 넣으면 되므로 O(1)이 걸리나, 만약 배열이 가득 찬 상태라면 더 큰 배열을 할당해서 기존의 배열을 새 배열로 옮겨야 하므로 O(n)만큼 걸린다. 삭제를 하고 난 후에 맨 뒤에 있는 원소를 삭제한 원소가 있던 위치에 위치시키면 별도의 위치 조정이 필요 없다.
연결 리스트가 정렬되어 있을 경우에는 탐색을 할 때 이진 검색을 사용할 수 있다. 하지만 배열과는 다르게 n / 2 지점에 바로 접근할 수 없기 때문에 O(n)의 시간 복잡도를 가진다.
이 비교를 통해서 얻을 수 있는 것은 배열을 하든 연결 리스트를 하든, 정렬을 하든 말든 반드시 하나 이상의 O(n)이 포함되어 있다는 것이다.
탐색, 삽입, 삭제의 속도를 골고루 줄일 수 있는 방법은 컴퓨터 공학 분야에서 활발하게 연구되었으며, 그에 대한 답 중 첫 번째가 이진 검색 트리, 레드 블랙 트리, AVL 트리와 같이 트리에 기반한 자료구조이고, 두 번째가 해시 테이블을 이용하는 것이다.(레드 블랙 트리와 AVL 트리는 이진 탐색 트리의 아이디어를 확장시킨 것이다)
이진 검색 트리(BST)
부모 노드는 최대 두 개의 자식 노드(왼쪽 노드와 오른쪽 노드는 서로 구분된다)를 가지고 있으며, 부모 노드는 왼쪽 서브 트리보다는 크며, 오른쪽 서브트리보다는 작다.

이진 탐색 트리와 힙의 차이
힙은 Complete Binary Tree의 구조를 가지고 있기 때문에 위 그림에 있는 트리는 힙이 될 수 없다. 또한 최대힙의 경우에는 모든 자식 노드가 부모 노드보다 작아야 하는 반면, 이진 탐색 트리의 경우에는 왼쪽 노드는 부모 노드보다 작아야 하지만 오른쪽 노드는 부모 노드보다 커야 한다.
트리의 순회
이진 검색 트리의 특성에 의해 중위 트리 순회(inorder tree walk)라고 하는 간단한 재귀 알고리즘을 통해서 이진 검색 트리의 모든 키를 정렬된 순서대로 출력할 수 있다.

이 알고리즘은 왼쪽 노드를 먼저 출력하고 루트 노드를 출력하고 오른쪽 노드를 출력한다는 규칙을 따름으로써 정렬된 순서로 출력할 수 있다.
전위 트리 순회(preorder tree walk)(루트-왼쪽-오른쪽), 후위 트리 순회(postorder tree walk)(왼쪽-오른쪽-루트)도 있다.
순회의 시간 복잡도를 구하기 위해 정이진트리(full binary tree)를 가정했다. 루트 노드를 제외한 n - 1은 왼쪽 노드, 오른쪽 노드로 나뉘어 재귀 함수를 실행시키고 있다. 그러므로 점화식을 작성해보면 다음과 같아진다.
$$T(n) = 2T(n / 2) - 1$$
마스터 정리에 의해 시간 복잡도는 O(n)이 된다.
탐색

위의 이진 탐색 트리에서 13을 찾는다고 하자.
1. 루트 노드와 먼저 비교한다. 13은 루트 노드인 15보다 작다. 그러므로 트리에 13이 있다면 그것은 루트 노드의 왼쪽 서브 트리에 있다.
2. 6과 비교한다. 13은 6보다 크므로 트리에 13이 있다면 그것은 6의 오른쪽에 있다.
3. 7과 비교한다. 13은 7보다 크므로 트리에 13이 있다면 그것은 7의 오른쪽에 있다.
4. 13과 비교한다. 동일하다.


코드를 재귀로 작성하든 반복문으로 작성하든 시간 복잡도는 똑같이 O(h)가 나온다(여기서 h는 트리의 높이. h는 최악의 경우 n과 같아질 수 있다).
최소값과 최대값
최소값은 루트 노드로부터 더 이상 왼쪽 노드가 없을 때까지 왼쪽 노드로 가면 발견할 수 있다. 반대로 최대값은 루트 노드로부터 더이상 오른쪽 노드가 없을 때 까지 오른쪽으로 가면 발견할 수 있다.


마찬가지로 O(h)의 시간 복잡도를 가진다.
Successor(직후 원소)
노드 x의 successor란 x보다 큰 것 중 가장 작은 노드를 말한다.
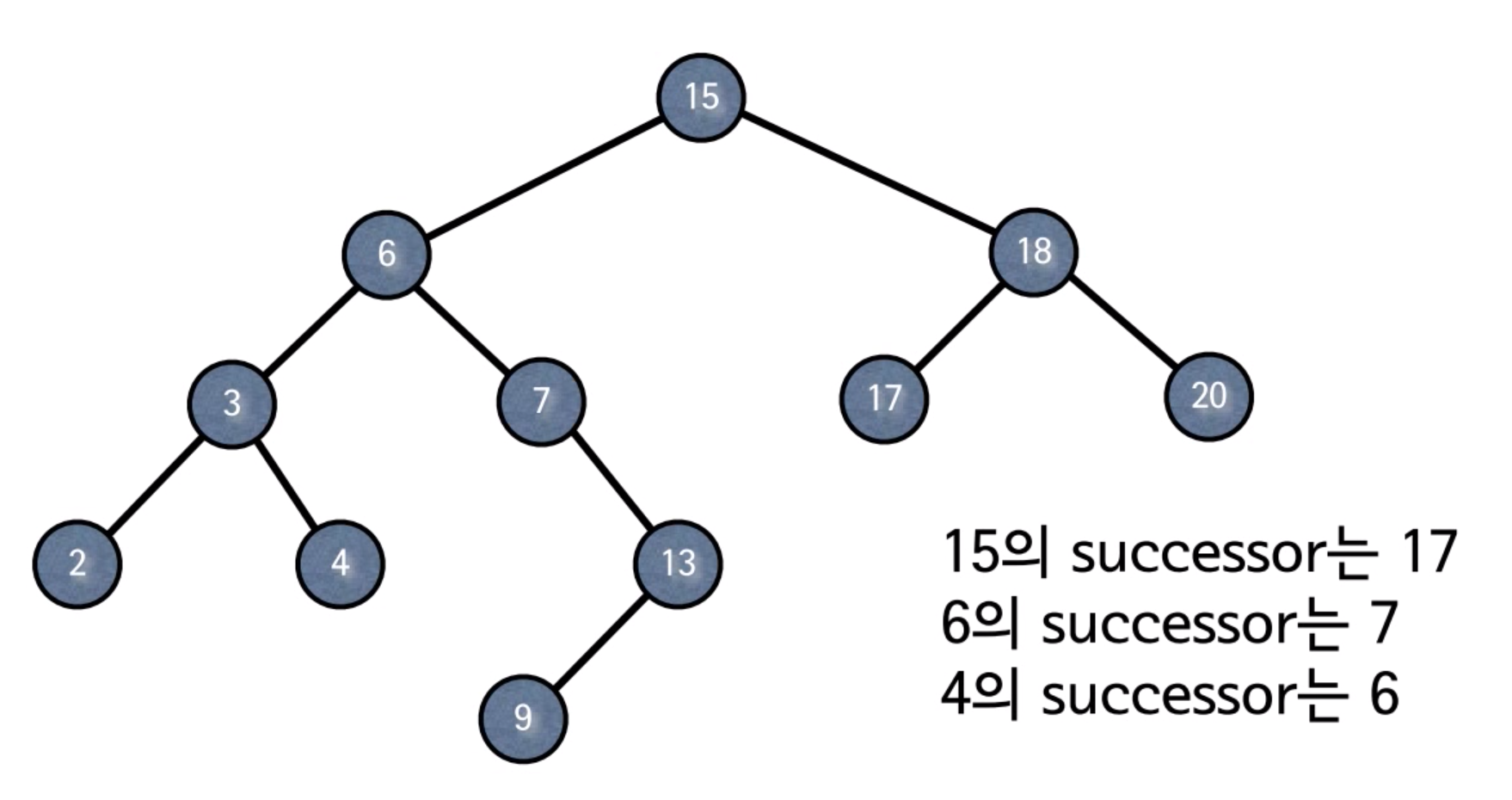
Successor에는 세 가지 경우가 있다.
1. 노드 x의 오른쪽 서브 트리가 존재하는 경우 - 오른쪽 서브트리의 최소값이 successor(ex. 15의 successor는 17)
2. 오른쪽 서브트리가 없는 경우에는 부모 노드로 올라간다. 올라가는 과정에서 오른쪽으로 올라가면 그때 successor를 만난다.(ex. 17의 successor는 18, 13의 successor는 15) 오른쪽으로 올라간다면 한 번에 successor를 만나고, 왼쪽으로 올라간다면 올라가다가 최초로 오른쪽으로 올라갔을 때 successor를 만난다.
3. 1, 2의 과정을 거쳤는데도 successor를 구하지 못했다면 successor는 없는 것이다.(ex. 20의 successor는 없다)

p[x]는 노드 x의 부모 노드다. 이 알고리즘의 시간 복잡도도 O(h)다.
predecessor(직전 원소)
노드 x의 predecessor란 x보다 작은 것 중 가장 큰 노드를 말한다. successor의 반대로 하면 된다.
삽입
위에서 배열로 데이터를 입력할 때는 입력 후에 원소들의 위치를 조정하는 작업을 했었고, 그것 때문에 O(n)의 시간 복잡도를 가졌다. 하지만 이진 탐색 트리를 활용한 삽입에서는 자리를 찾아가 추가하기만 하면 되므로 기존에 있던 원소들의 위치가 변함이 없다.

위 그림에서는 다음과 같은 과정을 거쳐 삽입된다.
1. 14는 루트 노드인 15보다 작으므로 왼쪽으로 간다.
2. 14는 6보다 크므로 오른쪽으로 간다.
3. 14는 7보다 크므로 오른쪽으로 간다.
4. 14는 13보다 크므로 오른쪽으로 간다.
5. 오른쪽 노드가 비었으므로 여기에 14를 추가해준다.

T가 트리이고, z가 삽입할 원소다. 9번째 줄에 y가 NIL일 경우를 예외로 하는 것을 볼 수 있다. y가 NIL이라는 것은 비어있는 트리라는 뜻이기 때문에 루트 노드에 z를 삽입하면 끝난다. 그렇지 않다면 비교를 통해 오른쪽이나 왼쪽에 삽입하면 된다. 시간 복잡도는 마찬가지로 O(h)다.
삭제
삭제 알고리즘은 두 가지가 있는데, 여기에서는 더 간단한 알고리즘을 다룬다. 삭제는 자식이 없는 경우, 자식이 하나 있는 경우, 자식이 둘 있는 경우로 나누어 알고리즘을 작성한다.
Case 1 : 자식이 없는 경우

Case 2 : 자식이 하나인 경우

자식이 하나만 있는 경우에는 그림과 같이 삭제할 원소의 부모 노드와 자식 노드를 이어 주기만 하면 된다. 7을 삭제해도 이진 탐색 트리의 규칙에 어긋나지 않는다.
Case 3 : 자식이 둘인 경우

자식이 둘인 경우는 복잡하다. 자식이 없거나 하나만 있는 경우에는 트리의 구조를 바꾸지 않고 삽입할 수 있었지만, 자식이 둘인 경우에는 트리의 구조가 바뀐다.
13을 지우는 것을 예를 들어 어떻게 삭제하는지 살펴보자.
1. 13을 바로 지우는 것은 어렵다. 6과 18이 부모 없는 노드가 되기 때문이다.
2. 그렇기 때문에 노드는 그대로 두고, 13이라는 데이터만 삭제한다.
3. 다른 노드로부터 데이터를 가져와 그 자리를 채워야 한다.
4. 이때 어떤 노드로부터 데이터를 가져와야 하는지에 대한 문제가 있다. 이진 검색 트리라는 것은 왼쪽 서브 트리는 부모 노드보다 작고, 오른쪽 서브트리는 부모 노드보다 크다는 특성을 만족해야 한다. 그렇기 때문에 13을 제거했을 때 다른 데이터로 채워야 한다면 그것은 최대한 13과 가까운 숫자여야 한다. 13에 가장 가까운 숫자는 successor이거나 predecessor이다. 어떤 것을 선택하든 문제없으며, 이 예제에서는 successor를 사용한다. 13의 successor가 13을 대체하게 되었으므로 13보다 큰 숫자이다. 그러므로 왼쪽 서브 트리보다 큰 값임은 확실하고, successor가 오른쪽 서브트리 중 가장 작은 값이기 때문에 오른쪽 서브트리보다 작은 것도 확실하다.
5. 그럼 원래 15가 있던 자리(successor의 자리)는 비게 된다. 그래서 다른 값으로 채워야 하는데, successor는 왼쪽 노드가 없다는 것이 보장되어 있다. 그러므로 successor의 자식 노드는 0개거나 1개다. 그러므로 Case 1이나 Case 2에 해당하므로 쉽게 해결할 수 있다.
그림으로 정리하면 다음과 같다.


1-3 라인에서는 z의 자식이 0개 혹은 1개인지 확인하는 것이다. 자식이 0개 혹은 1개인 경우에는 y에 z를 대입하고(Case 1, 2), 2개인 경우에는 y에 z의 successor를 대입한다(Case 3). y는 실제로 삭제하게 될 노드다.
4-13 라인이 y 노드를 삭제하는 과정이다.
y의 왼쪽 노드가 NIL이 아니라면 x는 y의 왼쪽 노드가 되고, NIL이라면 x는 y의 오른쪽 노드가 된다. (이때 x는 NIL이 되거나, 왼쪽 노드 혹은 오른쪽 노드가 된다)
x가 NIL이 아니라면 x의 부모는 삭제할 y의 부모가 된다.
만약 y의 부모가 NIL이라면, 즉, y가 루트 노드라면 x가 새로운 루트 노드가 된다. y의 부모가 NIL이 아니니라면, y가 부모 노드의 왼쪽 자식이었다면 x도 y의 부모 노드의 왼쪽 자식이 되고, y가 부모 노드의 오른쪽 자식이었다면 x도 y의 부모 노드의 오른쪽 자식이 된다.
14-17 라인은 Case 3에 해당되는 것으로, y에 있던 것을 z에 카피해주면 된다.
삭제의 경우에도 시간 복잡도는 O(h)다.
시간 복잡도 정리
탐색, 삽입, 삭제 연산의 평균적인 시간 복잡도는 O(h)다.
하지만 최악의 경우, 트리의 높이가 n이 될 수도 있으므로 시간 복잡도가 O(n)이 된다. 힘들게 코드를 작성했는데 최악의 경우가 발생한다면 아무 의미가 없다. 하지만 최악의 경우는 그렇게 빈번하게 발생하지 않는다. 평균적으로 O(h)의 시간 복잡도를 가진다는 것은 아주 훌륭한 자료구조다. (실제로 n개의 서로 다른 키를 갖는 임의로 만들어진 이진 탐색 트리의 높이의 기대값은 O(lgn)이다.)
정 아쉽다면 트리의 높이가 lgn을 넘지 않도록 레드 블랙 트리를 사용하면 된다. 레드 블랙 트리는 삽입하거나 삭제를 할 때 추가적인 작업을 해서 트리의 균형이 무너지지 않도록 해준다. 그래서 삽입이나 삭제 알고리즘은 조금 더 복잡해지지만 균형 잡힌 트리를 보장할 수 있다.
'자료구조 & 알고리즘' 카테고리의 다른 글
| [std]set, map (0) | 2019.05.10 |
|---|---|
| 에라토스테네스의 체 (0) | 2019.05.10 |
| 마스터 정리(Master Theorem) (0) | 2019.05.08 |
| 해시 테이블(Hash Table) (0) | 2019.05.05 |
| 힙정렬(Heap Sort) (0) | 2019.05.01 |
